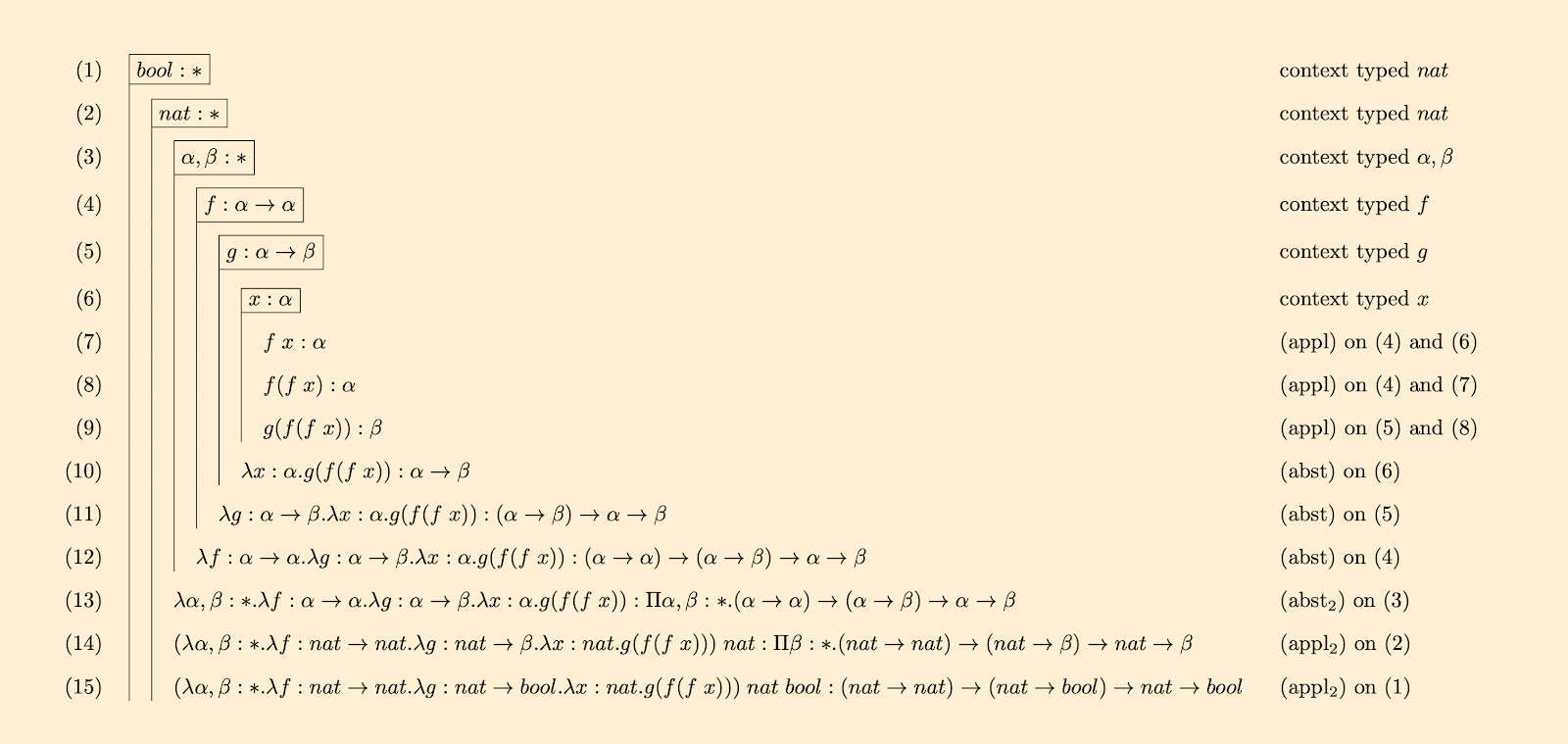Chapter 2 - Exercise 18

Exercise 2.18

Prove the Compatibility cases in the proof of Lemma 2.11.5.

Lemma 2.11.5 (Subject Reduction) is

If $Γ ⊢L : ρ$ and if $L \to _{β} L^′$, then $Γ ⊢L^′ : ρ$.

The proof of Lemma 2.11.5 is done by induction on the generation of $L \to_β L^′$. That is, all modes of constructing $L \to_β L^′$ are considered, and for each, we show that indeed, given $Γ ⊢L : ρ$ each mode of generating $L \to _{β} L^′$ leads to $Γ ⊢L^′ : ρ$.

There are four modes of generating $L \to_β L^′$, as follows.

(1) Basis. $(λx : σ. M)N →_β M[x := N]$

(2) Compatibility. If $M →_β N$, then $MK →_β NK$

(3) Compatibility. If $M →_β N$, then $KM →_β KN$

(4) Compatibility. If $M →_β N$, then $λx. M →_β λx. N$

The textbook provides a proof for the  (1) basis case. We'll provide the proofs for the compatibility cases (2-4).

(2) (Compatibility) If $M →_β N,$ then $MK →_β NK$

In this case $L ≡MK$ and $L^′ ≡NK$. 

So, we aim to show that if $Γ ⊢MK : ρ$ and if $MK \to _{β} NK$, then $Γ ⊢NK: ρ$.

We assume:

• the precursor is true, $M →_β N$, and
• induction hypothesis: if $Γ ⊢M : α$ and if $M \to _{β} N$, then $Γ ⊢N : α$

We start with

$$Γ ⊢ MK : ρ$$

Then by the Generation Lemma 2.10.7, we must have

$$ Γ ⊢ M :γ→ ρ \quad \land \quad Γ ⊢K : γ$$

The induction hypothesis tells us

$$Γ⊢N: γ→ρ$$

And so, finally,

$$Γ⊢NK:ρ$$

So we have shown that if $Γ ⊢MK : ρ$ and if $MK \to _{β} NK$, then $Γ ⊢NK: ρ$.

(3) (Compatibility) If $M →_β N,$ then $KM →_β KN$

In this case $L ≡KM$ and $L^′ ≡KN$. 

So, we aim to show that if $Γ ⊢KM : ρ$ and if $KM \to _{β} KN$, then $Γ ⊢KN: ρ$.

We assume:

• the precursor is true, $M →_β N$, and
• induction hypothesis: if $Γ ⊢M : α$ and if $M \to _{β} N$, then $Γ ⊢N : α$

We start with

$$Γ ⊢ KM : ρ$$

Then by the Generation Lemma 2.10.7, we must have

$$ Γ ⊢ K :γ→ ρ \quad \land \quad Γ ⊢M : γ$$

The induction hypothesis tells us

$$Γ⊢N: γ$$

And so, finally,

$$Γ⊢KN:ρ$$

So we have shown that if  $Γ ⊢KM : ρ$ and if $KM \to _{β} KN$, then $Γ ⊢KN: ρ$.

(4) Compatibility. If $M →_β N$, then $λx. M →_β λx. N$

In this case $L ≡λx. M$ and $L^′ ≡λx. N$. 

So, we aim to show that if $Γ ⊢λx. M : ρ$ and if $λx. M \to _{β} λx. N$, then $Γ ⊢λx. N: ρ$.

We assume:

• the precursor is true, $M →_β N$, and
• induction hypothesis: if $Γ ⊢M : α$ and if $M \to _{β} N$, then $Γ ⊢N : α$

We start with

$$Γ ⊢λx. M : ρ$$

Then by the Generation Lemma 2.10.7, we must have

$$ Γ, x:α ⊢ M :β \quad \land \quad ρ \equiv α→β$$

The induction hypothesis tells us

$$Γ, x:α ⊢N: β$$

And so, finally,

$$Γ ⊢λx. N : ρ$$

So we have shown that if $Γ ⊢λx. M : ρ$ and if $λx. M \to _{β} λx. N$, then $Γ ⊢λx. N: ρ$.

Chapter 2 - Exercise 17

Exercise 2.17

Prove Lemma 2.10.9 (the ‘Uniqueness of Types Lemma’).

(Hint: use Lemma 2.10.7 (the ‘Generation Lemma’).)

The Uniqueness of Types Lemma 2.10.9 is:

Assume $Γ ⊢M : σ$ and $Γ ⊢M : τ$. Then $σ ≡τ$.

The Generation Lemma 2.10.8 is:

(1) If $Γ ⊢x : σ$, then $x : σ ∈ Γ$

(2) If $Γ ⊢MN : τ$, then there is a type $σ$ such that $Γ ⊢ M : σ →τ$ and $Γ ⊢N : σ$

(3) If $Γ ⊢λx : σ. M : ρ$, then there is $τ$ such that $Γ, x : σ ⊢M : τ$ and $ρ ≡σ →τ$.

All λ-terms are the result of being constructed by one of the (var), (appl) or (abst) rules, as per the Derivation rules of Definition 2.4.5. This means we can use structural induction for each of these three modes of constructing an arbitrary λ-term.

(var)-rule

If $Γ⊢x:α$ and $Γ⊢x:β$ are the results of the (var) rule, then the context $Γ$ must contain $x:α$ and $x:β$, by the Generation Lemma.

To be well-formed, there can only be one $x$ in $Γ$ and so $x:α \equiv x:β$, which means $α \equiv β$.

(appl)-rule

If $Γ⊢AB:α$ and $Γ⊢AB:β$ are the results of the (appl) rule, then as premises to the (appl) rule we must have, by the Generation Lemma, 

$$Γ⊢A:γ→α \quad \text{and} \quad Γ⊢B:γ$$

$$Γ⊢A:σ→β \quad \text{and} \quad Γ⊢B:σ$$

As an induction hypotheses we assume the uniqueness of types applies to these premises. That means

$$γ→α \equiv σ→β$$

$$γ \equiv σ$$

The first gives us $α \equiv β$. Thus we have shown that the type of $AB:α$ and $AB:β$ are the same.

(abst)-rule

If $Γ⊢λx:σ.M:α$ and $Γ⊢λx:σ.M:β$ are the results of the (abst) rule, then the premises to the (abst) rule must be, by the Generation Lemma,

$$Γ, x:σ⊢M:γ \qquad \text{and} \qquad {α \equiv σ→γ}$$

$$Γ, x:σ⊢M:ρ \qquad \text{and} \qquad {β \equiv σ→σ}$$

As an induction hypotheses we assume the uniqueness of types for these premises. This gives us $ γ \equiv ρ $, which immediately gives us $α \equiv β$. 

Thus $Γ⊢λx:σ.M:α$ and $Γ⊢λx:σ.M:β$ have the same type.

By showing the uniqueness lemma holds for each mode of construction, we have shown it holds for arbitrary λ-terms.

Chapter 2 - Exercise 16

Exercise 2.16

Prove Lemma 2.10.8 (the ‘Subterm Lemma’).

Let's remind ourselves of Lemma 2.10.8,  the Subterm Lemma.

If M is legal, then every sub-term of M is legal.

Definition 1.3.5 defines sub-terms of λ-terms.

(1) (Basis) $Sub(x) = {x}$, for each $x ∈V$.

(2) (Application) $Sub((MN)) = Sub(M)∪Sub(N)∪{(MN)}$.

(3) (Abstraction) $Sub((λx. M)) = Sub(M)∪{(λx. M)}$.

We start by noting that all λ-terms are at the top level one of three forms, a variable, an application, or an abstraction. We can therefore use the (var), (appl) and (abst) construction rules in a structural induction proof.

(var)-rule

We'll consider a precursor judgement $Γ⊢M:α$ from which the (var) rule results in $Γ⊢x:β$ where $x:β \in Γ$.

Our aim is show that if $x$ is legal, then every sub-term of $x$ is legal.

This is trivially true.

Note that we didn't need to use an induction hypothesis.

(appl)-rule

We'll consider two precursors $Γ⊢A;α→β$, and $Γ⊢B:α$. Here $A$ and $B$ are legal terms, a premise for the (appl) rule which gives us $Γ⊢AB:β$.

As an induction hypothesis we'll assume that if $A$ and $B$ are legal, then both their sub-terms are legal.

Our aim is to show that if $AB$ is legal, then every sub-term of $AB$ is legal. 

Definition 1.3.5 tells us the sub-terms of $AB$ are $AB$ itself, and the sub-terms of $A$ and $B$. We have $AB$ is legal by assumption. The remain options $A$ and $B$ have legal sub-terms by the induction hypothesis.

(abst)-rule

We'll consider the precursor $Γ, x:α⊢M:β$. Here $M$ is a legal term, a premise for the (abst) rule which gives us $Γ⊢λx.M:α→β$.

As an induction hypotheses we'll assume that if $M$ is legal, then every sub-term of $M$ is legal.

Our aim is to show that if $λx.M$ is legal, then every sub-term of $λx.M$ is legal.

Definition 1.3.5 tells us the sub-terms of $λx.M$ is $λx.M$ itself, and the sub-terms of $M$. The term $λx.M$ is legal by assumption. The induction hypothesis tells us $M$ is legal and so are its sub-terms.

We've shown that if a λ-term is legal, then all its sub-terms are legal, but showing this is true for all three modes of constructing that λ-term.

Chapter 2 - Exercise 15

Exercise 2.15

Give the (var)- and (appl)-cases of the proof of Lemma 2.10.5(1) (the ‘Thinning Lemma’).

Let's remind ourselves of Lemma 2.10.5(1):

(1) (Thinning) Let $Γ^′$ and $Γ^{′′}$ be contexts such that $Γ^′ ⊆Γ^{′′}$. If $Γ^′ ⊢M : σ$, then also $Γ^{′′} ⊢M : σ$.

Quoting the textbook, to prove a general property $P$ for an arbitrary expression $E$ we can proceed by:

• assuming that $P$ holds for all expressions $E^{\prime}$ used to construct $E$ (the induction hypothesis),
• and then proving that $P$ also holds for $E$ itself.

Another simple explanation and illustration of structural induction is here (link).

(var)-case

The (var) rule applied to the precursor judgement

$$J_1 := Γ^′ ⊢ M : ρ$$

produces a new judgement

$$K _1:= Γ^′ ⊢ x : σ$$

if $x:σ \in Γ^′$.

For an induction hypothesis, we assume the Thinning Lemma holds for the precursor judgement $J_1$. That is,

$$J_1 := Γ^′ ⊢ M : ρ  \quad \land \quad (Γ^′ \subseteq Γ^{′′}) \quad \implies \quad J_2 := Γ^{′′} ⊢ M : ρ $$

We need to show that the Thinning Lemma holds for the judgement $K_1$ as follows

$$K_1 := Γ^′ ⊢ x : σ  \quad \land \quad (Γ^′ \subseteq Γ^{′′}) \quad \implies \quad K_2 := Γ^{′′} ⊢ x : σ $$

Since $x:σ \in Γ^′$ and $Γ^′ \subseteq Γ^{′′}$, it must be that $x:σ \in Γ^{′′}$. Therefore $Γ^{′′} ⊢ x : σ$, and so the judgement $K_2$ is true.

We have shown that if the Thinning Lemma holds for a judgement, it also holds for the judgement resulting from applying the (var) constructor to it, and therefore holds for all judgements produced by the (var) constructor.

(appl)-case

The (appl) rule applied to two precursor judgements

$$J_1 := Γ^′ ⊢ M : α→β \quad \text {and} \quad J_2 := Γ^′ ⊢ N : α $$

produces a new judgement

$$K _1:= Γ^′ ⊢ MN : β$$

For an induction hypothesis, we assume the Thinning Lemma holds for the two precursor judgements $J_1$ and $J_2$. That is,

$$J_1 := Γ^′ ⊢ M : α→β  \quad \land \quad (Γ^′ \subseteq Γ^{′′}) \quad \implies \quad J_3 := Γ^{′′} ⊢ M : α→β $$

$$J_2 := Γ^′ ⊢ N : α  \quad \land \quad (Γ^′ \subseteq Γ^{′′}) \quad \implies \quad J_4 := Γ^{′′} ⊢ N : α $$

We need to show that the Thinning Lemma holds for the judgement $K_1$ as follows

$$K _1:= Γ^′ ⊢ MN : β  \quad \land \quad (Γ^′ \subseteq Γ^{′′}) \quad \implies \quad K_2 := Γ^{′′} ⊢ MN : β $$

Applying the (appl) rule to $J_3$ and $J_4$ gives us this desired judgement $K_2$.

We have shown that if the Thinning Lemma holds for two judgements, it also holds for the judgement that results from the (appl) rule applied to both of them, and therefore holds for all judgements resulting from the (appl) constructor.

Chapter 2 - Exercise 14

Exercise 2.14

Find an inhabitant of the type $α →β →γ$ in the following context:

$Γ ≡ x : (γ →β) →α →γ$

Give an appropriate derivation.

The inhabitant we're looking for takes two arguments, and $x$ doesn't match their type, so let's set $ y:α, \; z: β, \; t:γ $.

We construct $λt.z$ which has type $(γ→β)$. If we apply $x$ to this we have $x(λt.z)$ of type $α→γ$. We can apply the combined expression to $y$, which gives us $x(λt.z)y$ which has type $γ$, as desired. All that remains is to abstract on $z$ and then $y$ to give us the following judgement.

$$ x : (γ →β) →α →γ \quad \vdash \quad  λy:α.λz:β.x(λt:γ.z)y : α →β →γ$$

The following flag notation proof provides clarity to the above discussion.

Chapter 2 - Exercise 13

Exercise 2.13

Find a term of type $τ$ in context $Γ$, with:

(a) $τ ≡(α →β) →α →γ, \quad Γ ≡x : α →β →γ$

(b) $τ ≡α →(α →β) →γ, \quad Γ ≡x : α →β →α →γ$

(c) $τ ≡(α →γ) →(β →α) →γ, \quad Γ ≡x : (β →γ) →γ$

Give appropriate derivations.

(a) The derivation below shows the term is

$$\lambda y:\alpha \to \beta.\lambda z:\alpha.xy$$

such that

$$ x: \alpha \to \beta \to \gamma \quad \vdash \quad \lambda y:\alpha \to \beta.\lambda z:\alpha.xy: (\alpha \to \beta) \to \alpha \to \gamma$$

(b) The derivation below shows the term is

$$  \lambda y:\alpha.\lambda z:\alpha \to \beta.(xz)y $$

such that

$$ x : α →β →α →γ \quad \vdash \quad  \lambda y:\alpha.\lambda z:\alpha \to \beta.(xz)y : : \alpha \to (\alpha \to \beta) \to \gamma $$

(c) The derivation below shows the term is

$$ \lambda y: \alpha \to \gamma.\lambda z:\beta \to \alpha.(xz)y $$

such that

$$ x: (\beta \to \gamma) \to \beta \quad \vdash \quad  \lambda y: \alpha \to \gamma.\lambda z:\beta \to \alpha.(xz)y: ( \alpha \to \gamma) \to (\beta \to \alpha) \to \gamma $$

Chapter 2 - Exercise 12

Exercise 2.12

(a) Construct a term of type $((α →β) →α) →(α →α →β) →α$

(b) Construct a term of type $((α →β) →α) →(α →α →β) →β$

(a) The term takes two arguments, so let's set $x:((α →β) →α)$ and $y:(α →α →β)$.

We can't apply $x$ to $y$ or vice versa, so we'll construct $z:α$. 

This gives us $yz : α→β$, and so $yzz:β$. This means $λz:α.yzz : α→β$. Finally, $x(λz:α.yzz): α$, as desired. 

An abstraction with $y$ then $x$ gives us the required term.

$$ λx:((α →β) →α) . λy: (α →α →β) . x(λz:α. yzz) : ((α →β) →α) →(α →α →β) →α $$

(b) The term take the same two arguments, so again let's set $x:((α →β) →α)$ and $y:(α →α →β)$.

We'll use the previous result that  $x(λz:α.yzz): α$. 

Applying $y$ to two of these expressions gives us $y (x(λz:α.yzz)) (x(λz:α.yzz)) : β$,  the desired type.

Again, abstracting with $y$ then $x$, gives us the required term. 

$$ λx:((α →β) →α) . λy: (α →α →β) . y (x(λz:α.yzz)) (x(λz:α.yzz)) : ((α →β) →α) →(α →α →β) →β$$

Chapter 2 - Exercise 11

Exercise 2.11

Find inhabitants of the following types in the empty context, by giving appropriate derivations.

(a) $(α →α →γ) →α →β →γ$

(b) $((α →γ) →α) →(α →γ) →β →γ$

(a) The term takes 3 arguments so let's start with $x:α →α →γ, y:α, z:β$. 

We can immediately see that $x$ takes arguments of type $α$ twice we can construct $xyy:γ$. The third argument $z:β$ is taken but ignored. So we have the following.

$$ λx:α →α →γ . λy:α . λz:β . xyy : (α →α →γ) →α →β →γ $$

The following flag notation derivation confirms the inhabitant has the given type.

(b) Again the term takes 3 arguments so let's start with $x:((α →γ) →α) , y:(α→β), z:β$.

We can see that $x$ takes an argument of type $(α→γ)$, and $y$ is for this type. We can construct $xy:α$. Since $y$ takes an argument of type $α$ and returns a type $γ$, means we can further construct $y(xy):γ$. The third argument $z:β$ is taken but ignored. So we have the following.

$$ λx:(α →γ) →α . λy:α→γ . λz:β . y(xy) : ((α →γ) →α ) →(α→β) →β →γ $$

The following flag notation derivation confirms the inhabitant has the given type.

Chapter 2 - Exercise 10

Exercise 2.10

Prove that the following pre-typed λ-terms are legal, by giving derivations in (shortened) flag notation.

(a) $xz(yz)$

(b) $λx : (α →β) →β. x(yz)$

(c) $λy : α. λz : β →γ. z(xyy)$

(d) $λx : α →β. y(xz)z$

(a) All of the variables are not pre-typed, they are all free variables. We need to show the λ-term is type-able by finding suitable types for these free variables. 

Before we start, let's parenthesise the term for greater clarity as $(xz)(yz)$.

Let's start with $x:A, y:B, z:C$. Since $y$ is applied to $z$, we have $B=C \to D$. Similarly, since $x$ is applied to $z$, we have $A = C \to E$. And since $xz$ is applied to $yz$, we have $E=D \to F$.

Summarising, and renaming the variables, we have 

$$ x: α \to β \to γ, y: α \to β, z: α \quad \vdash \quad xz(yz) : γ$$

The following flag notation derivation confirms the λ-term is legal.

The λ-term is legal because there exists a context such that the term has a type (is type-able).

(b) We're given $x:(α →β) →β$, so let's set $y:B, z:C$. Since $y$ is applied to $z$, we have $B=C \to D$. And since $x$ is applied to $(yz)$ we have $(α →β) →β = D \to E$. So $E=β$ and $D=(α→β)$. Considering $B$ again, we have $B=C \to (α→β)$.

In summary,  and renaming the variables, we have

$$ y: γ → (α →β), z: γ \quad \vdash \quad λx : (α →β) →β. x(yz) : ((α →β) →β) → β$$

The following flag notation derivation confirms the λ-term is legal.

(c) We're given $y : α$ and $z : β →γ$, so let's set $x:A$. Since $x$ is applied to $y$, we have $A=α →B$. We have $xy$ applied to $y$ which means $B=α→D$. Finally, $z$ is applied to $(xyy)$ so $β→γ$ must be the same as $D→γ$. This means $D=β$,  $B=α→β$, and $A=α→α→β$.

In summary, and renaming variables, we have

$$ x:α→α→β \quad \vdash \quad λy : α. λz : β →γ. z(xyy) : α→(β →γ) →γ $$

The following flag notation derivation confirms the λ-term is legal.

(d) We're given $x:α→β$, so let's set $y:B, z:C$. Since $x$ is applied to $z$ we have $C=α$. Since $y$ is applied to $(xz)$ we have $B=β→D$. Finally $y(xz)$ is applied to $z$ we have $D=α→E$.

In summary, and renaming variables, we have

    $$ λy: β→α→γ, z:α \quad \vdash \quad λx:α→β.y(xz)z: (α→β)→γ $$

The following flag notation derivation confirms the λ-term is legal.

Chapter 2 - Exercise 9

Exercise 2.9

Give derivations by means of which the following judgements become type-checked. You may use the flag notation. In part (b), you may use flag notation in its ‘shortened’ form, i.e. suppress steps involving the (var)-rule.

(a) $x : δ→δ→α, y : γ→α, z : α→β ⊢ λu : δ. λv : γ. z(yv) : δ →γ →β$

(b) $x : δ→δ→α, y : γ→α, z : α→β ⊢ λu : δ. λv : γ. z(xuu) : δ →γ →β$

(a) The following flag notation proof confirms the judgement is type-checked (click to enlarge).

(b) The following flag notation proof confirms the judgement is type-checked.

Chapter 2 - Exercise 8

Exercise 2.8

(a) Add types to the bound variables in the λ-term $λxy. y(λz. yx)$ such that the type of this term becomes

$$(γ →β) →((γ →β) →β) →β$$

(b) Give a derivation in tree format, proving this.

(c) Sketch a diagram of the tree structure, as in Section 2.5.

(d) Transform the derivation into flag format.

(a) Let's first establish the types variables, all of which happen to be bound. The desired term tells us the type of $x$ and $y$. These are $x:γ → β$ and $y:((γ→β)→β)$. We can use these to narrow down the type of $z$. Lets label the type of $z$ as $α$.

Given these known types, the type of $yx$ must be $β$.  The type of $(λz.yx)$ must therefor be $α→β$. Since $y:((γ→β)→β)$ is applied to $(λz.yx):α→β$, this tells us $γ=α$. 

To summarise, pre-typed λ-term is.

$$λx:γ→β.y:(γ→β)→β. y(λz:γ. yx)$$

(b) The following is derivation to confirm the type of the above γ-term.

(i) (var) gives us x:γ→β

(ii) (var) gives us y:(γ→β)→β

(iii) (appl) on (i) and (ii) gives us yx:β

(iv) (abst) gives us λz.yx:γ→β

(v) (appl) on (iv) and (ii) gives us $y(λz. yx):β$

(vi) (abst) gives us $λy.y(λz. yx):((γ→β)→β)→β$

(vii) (abst) gives us $λxy.y(λz. yx):(γ→β)→((γ→β)→β)→β$ as required.

(c) The following is a tree diagram showing the structure of the proof (click to enlarge).

(d) The following is the derivation in flag-format (click to enlarge).

Chapter 2 - Exercise 7

Exercise 2.7

(a) Prove the following by giving a kind of derivation, with the rules (func-appl) and (func-abst) described in Example 2.4.8:

If $f : A \to B$ and $g : B \to C$, then $g \circ f : A \to C$.

Note: $g \circ f$ is the composition of $f$ and $g$, being the function mapping $x$ to $g(f x)$.

(b) Give a derivation in natural deduction of the following expression, using the rules ⇒-elim and ⇒-intro described in Example 2.4.9:

$$(A ⇒B) ⇒((B ⇒C) ⇒(A ⇒C))$$

(c) Prove that the following pre-typed λ-term is legal, using the flag format:

$$λz : α. y(xz)$$

(d) Indicate the similarities between the derivations in (a), (b) and (c).

---

(a) We read $f : A \to B$ as $f$ is a member of the set $A \to B$, the set of all functions from $A$ to $B$.

We start by introducing a variable $x \in A$. This means we can apply the (func-appl) rule.

$$ (func-appl) : \frac{f: A \to B \; \land \; x \in A}{f(x) \in B} $$

This rules lets us conclude that $f(x)$ is a member of $B$.

Next we read $g : B \to C$ as $g$ is a member of the set $B \to C$, the set of all functions from $B$ to $C$. Since w now have $f(x) \in B$, we can use this in the next application of the (func-appl) rule.

$$ (func-appl) : \frac{g: B \to C \; \land \; f(x) \in B}{g(f(x)) \in C} $$

This tells us $g \circ f$ maps from $A \to C$.

---

(b) To show $P \implies Q$ we assume $P$ and derive $Q$.

Here this means we assume $(A \implies B)$ and derive $(B \implies C) \implies (A \implies C)$.

But to derive $(B \implies C) \implies (A \implies C)$ we assume $(B \implies C$ is true and derive $(A \implies C)$. And to do that, we assume $A$ is true and derive $C$.

We can do that because $A$ and $(A \implies B)$ gives us $B$ by the elimination rule. Similarly $B$ and $(B \implies C)$ gives us $C$ by the elimination rule. 

So we have $(A \implies C)$ by the introduction rule, and $(B \implies C) \implies (A \implies C)$ by introduction again. One more introduction gives us $(A ⇒B) ⇒((B ⇒C) ⇒(A ⇒C))$.

The above argument is a little informal. More properly, we need to keep track of assumptions and discharging them with the elimination rule.

The following proof tree provides this clarity.

---

(c) To prove the pre-typed λ-term is legal, we need to show there exists a context $Γ$ such that $Γ⊢M:ρ$ where $M$ is the term and $ρ$ is the type. 

Let's consider the following context.

$$Γ := y: \beta \to \gamma, x: \alpha \to \beta, z:\alpha$$

We then apply the derivation rules from Definition 2.4.5:

$(i) \quad y: \beta \to \gamma, \; x: \alpha \to \beta, \; z:\alpha \quad \vdash \quad z:\alpha \quad $ (var)

$(ii) \quad y: \beta \to \gamma, \; x: \alpha \to \beta, \; z:\alpha \quad \vdash \quad x:\alpha  \to \beta \quad $ (var)

$(iii) \quad y: \beta \to \gamma, \; x: \alpha \to \beta, \; z:\alpha \quad \vdash \quad xz: \beta \quad $ (appl) on (i) and (ii)

$(iv) \quad y: \beta \to \gamma, \; x: \alpha \to \beta, \; z:\alpha \quad \vdash \quad y:\beta  \to \gamma \quad $ (var)

$(v) \quad y: \beta \to \gamma, \; x: \alpha \to \beta, \; z:\alpha \quad \vdash \quad y(xz):\gamma \quad $ (apppl) on (iv) and (iii)

$(vi) \quad y: \beta \to \gamma, \; x: \alpha \to \beta  \quad \vdash \quad \lambda z:\alpha.y(xz) : \alpha \to \gamma \quad $ (var)

Thus we have shown the λ-term is legal because there exists a context, $Γ$ from which the λ-term is derivable and has a type $\alpha \to \gamma$.

The following shows this in flag format (click to enlarge).

---

(d) TODO

Chapter 2 - Exercise 6

Exercise 2.6

(a) Prove that the following pre-typed λ-term is legal, using the tree format:

$$λx : ((α →β) →α). x(λz : α. y)$$

(b) Transform the derivation into flag format.

For clarity, it is useful to write the lambda term without the types:

$$λx. x(λz. y)$$

(a) To prove the pre-typed λ-term is legal, we need to show there exists a context $Γ$ and type $ρ$ such that $Γ \vdash M : ρ$, where $M$ is the given λ-term.

Let's try the following context

$$Γ := x: (α →β) →α, y: β, z:α$$

We'll now try to apply the 3 Derivation rules of simply typed calculus from Definition 2.4.5, which are (var), (appl) and (abst).

$(i) \quad x: (α →β) →α, \; y: β, z:α \quad \vdash \quad y: β \quad $ (var)

$(ii) \quad x: (α →β) →α, y: β \quad \vdash \quad λz:α.y : α→β \quad $ (abst) on (i)

$(iii) \quad x: (α →β) →α, \; y: β \quad \vdash \quad x: (α →β) →α \quad $ (var)

$(iv) \quad x: (α →β) →α, \; y: β \quad \vdash \quad x(λz:α.y): α \quad $ (appl) on (iii) and (ii)

$(v) \quad y: β \quad \vdash \quad (iv) \quad  λx : ((α →β) →α). x(λz:α.y): ((α →β) →α) → α \quad $ (abst) on (iv)

Through an application of the Derivation rules, we've shown there exists a context $Γ$ and type $ρ$ such that $Γ \vdash M : ρ$. The context is $Γ := x: (α →β) →α, y: β, z:α$ and the type is $ρ := α$. This means the λ-term is indeed legal.

The following is a tree diagram summarising the structure of the proof (click to enlarge).

(b) The following is the derivation in flag format (click to enlarge).

Chapter 2 - Exercise 5

Exercise 2.5

For each of the following terms, try to find a pre-typed variant which is typable. If this is not possible, show why.

(a) $λxy. x(λz. y)y$

(b) $λxy. x(λz. x)y$

(a) Let's try to work out the types for $λxy. x(λz. y)y$. 

We start with the bound variables $x:A, y:B, z:C$. 

The type of $(λz. y)$ is $C \to B$, and since $x$ is applied to it, we must have $A = (C \to B) \to D$. Finally, since $x(λz. y)$ is applied to $y$, we have $D = B \to E$.

Summarising we have

$$ λxy. x(λz. y)y : ((C \to B) \to B \to E)  \to B  \to E$$

Renaming variables, and writing as a pre-typed λ-term, we have

$$ λx:((\gamma \to β) \to β \to ρ).λy:β. x(λz:\gamma. y)y$$

(b) Let's try to work out the types for $λxy. x(λz. x)y$.

We start with the bound variables $x:A, y:B, z:C$. 

The type of $(λz. x)$ is $C \to A$, and since $x$ is applied to it, this leads to $A = (C \to A)$, which is impossible.

So $λxy. x(λz. x)y$ is not typable.

Chapter 2 - Exercise 4

Exercise 2.4

Add types to the bound variables in the following λ-terms such that they become pre-typed λ-terms which are legal, and give their types:

(a) $λxyz. x(yz)$

(b) $λxyz. y(xz)x$

(a) Let's first work out the types for $λxyz. x(yz)$.

We start with $x:A, y:B, z:C$. Since $y$ is applied to $z$ we have $B = C \to D$, and the type of $(yz)$ is D. Since $x$ is applied to $(yz)$ we must have $A = D \to E$. 

Let's summarise this.

$$ (D \to E) \to (C \to D) \to C \to E $$

Renaming variables, and writing as a pre-typed λ-term we have

$$ λx: (β \to \gamma).λy: (α \to β).λz: α . x(yz) $$

The type is

$$(β \to \gamma) \to (α \to β) \to α \to \gamma$$

(b) Let's now work out the types for $λxyz. y(xz)x$.

We start with $x:A, y:B, z:C$. The sub-term $(xz)$ tells us $A=C \to D$. Since $y$ is applied to $(xz)$ we must have $B=D \to E$. Finally, $y(xz)$ is applied to $x$ so $E=A \to F$. 

Let's summarise this.

$$(C \to D) \to (D \to (C \to D) \to F) \to C \to F$$

Renaming variables, and writing as a pre-typed λ-term we have

$$ λx: (α \to β).λy:(β \to (α \to β) \to \gamma).λz:α. y(xz)x $$

The type is

$$(α \to β) \to (β \to (α \to β) \to \gamma)  \to α \to \gamma$$

Chapter 2 - Exercise 3

Exercise 2.3

Find types for $K$ and $S$ (see Exercise 1.9).

Let's remind ourselves of $K$ and $S$.

$$\begin{align} K &:= λxy. x \\ \\  S &:= λxyz. xz(yz) \end{align}$$

Let's start with $ K := λxy. x $.

Let's take the type of $x$ as $A$, and the type of $y$ as $B$. Then the type of $K$ is simply

$$K : A \to B \to A$$

Now consider $S := λxyz. xz(yz) $.

Let's parenthesise the term to make its meaning clearer.

$$S := λxyz. (xz)(yz) $$

Let's take the types of the variables as 

$$x:A,\; y:B, \; z:C$$

Since $x$ is applied to $z$, and $y$ is applied to $z$, we have

$$\begin{align} A & = C \to D \\ \\ B & = C \to E \end{align}$$

This means the type of $(xz)$ is $D$, and since $(xz)$ is applied to $(yz)$ which has type $E$, the type of $(xz)$ must be $D = E \to F$.

Let's put this together.

$$S : (C \to (E \to F)) \to (C \to E) \to C \to F$$

Let's rename the variables to make it easier to read.

$$S : (B \to (A \to C)) \to (B \to A) \to B \to C$$

Note: I had help to think more systematically about this kind of problem here (link).

Chapter 2 - Exercise 2

Exercise 2.2

Find types for zero, one and two (see Exercise 1.10).

Let's remind ourselves of what these Church numerals are;

$$\begin{align} zero &:= λfx.x \\ \\ one &:= λfx.fx \\ \\ two &:= λfx.f(fx) \end{align}$$

$zero := λfx.x$

If $x:A$ and $f:B$, then the type of zero is

$$zero : B \to A \to A$$

$one := λfx.fx$

If $x:A$ then $f$ must have compatible type $f:A \to B$.

The type of one is

$$one : (A \to B) \to A \to B$$

$two := λfx.f(fx)$

If $x:A$ then $f$ must have compatible type $f:A \to B$. But $f$ is also applied to $(fx)$ so it must have type $A \to A$.

The type of two is

$$two : (A \to A) \to A \to A$$

Chapter 2 - Exercise 1

Exercise 2.1

Investigate for each of the following λ-terms whether they can be typed with a simple type. If so, give a type for the term and the corresponding types for $x$ and $y$. If not, explain why.

(a) $xxy$

(b) $xyy$

(c) $xyx$

(d) $x(xy)$

(e) $x(yx)$

(a) Let's clarify $xxy$ as $(xx)y$. 

We know from Example 2.2.26(3) that $xx$ can't be typed. The reason is that if the type of the second $x$ is $A$, then the type of the first $x$ must be $A \to B$, and these two can't be unified.

So $xxy$ can't be simply typed.

(b) Let's clarify $xyy$ as $(xy)y$.

If the type of the second $y$ is $A$, then the type of $(xy)$ must be $A \to B$.

If the type of the first $y$ is $C$, then the type of $x$ must be $C \to D$.

Unifying, we have $A = C$ and $D = A \to B$.

So the types are:

$$\begin{align} y &: A \\ \\  x &: A \to (A \to B) \\ \\  xyy &: B \end{align}$$

(c) Let's clarify $xyx$ as $(xy)x$.

If the type of the second $x$ is $A$, then the type of $(xy)$ must be $A \to C$.

If the type of $y$ is $B$, then the type of the first $x$ must be $B \to D$.

Unifying, we have $A = B \to D$, and $D = A \to C$.

We can't resolve these to simple types because, for example, the type $A$ is infinitely self-referential. That is, 

$$\begin{align} A &= B \to D \\ \\ & =  B \to (A \to C) \\ \\ & =  B \to ((B \to D) \to C) \\ \\ & =  B \to ((B \to (A \to C)) \to C)  \\ \\ & = \ldots  \end{align}$$

So $xyx$ can't be simply typed.

(d) The term $x(xy)$ is already parenthesised.

If the type of $y$ is $B$, then the the type of the second $x$ must be $B \to C$.

That means the type of $(xy)$ is $C$.

Which means the type of the first $x$ must be $C \to D$.

Unifying, we have $B = C = D$.

So the types are:

$$\begin{align} y &: B \\ \\  x &: (B \to B) \\ \\  x(xy) &: B \end{align}$$

(e) The term $x(yx)$ is already parenthesised.

If the type of the second $x$ is $A$, then the type of $y$ is $A \to C$.

This means the type of $(yx)$ is $C$.

The type of the first $x$ must then be $C \to D$.

Unifying, we have $A =C \to D$.

So the types are:

$$\begin{align} x &: C \to D \\ \\  y &: (C \to D) \to C \\ \\  x(yx) &: D \end{align}$$