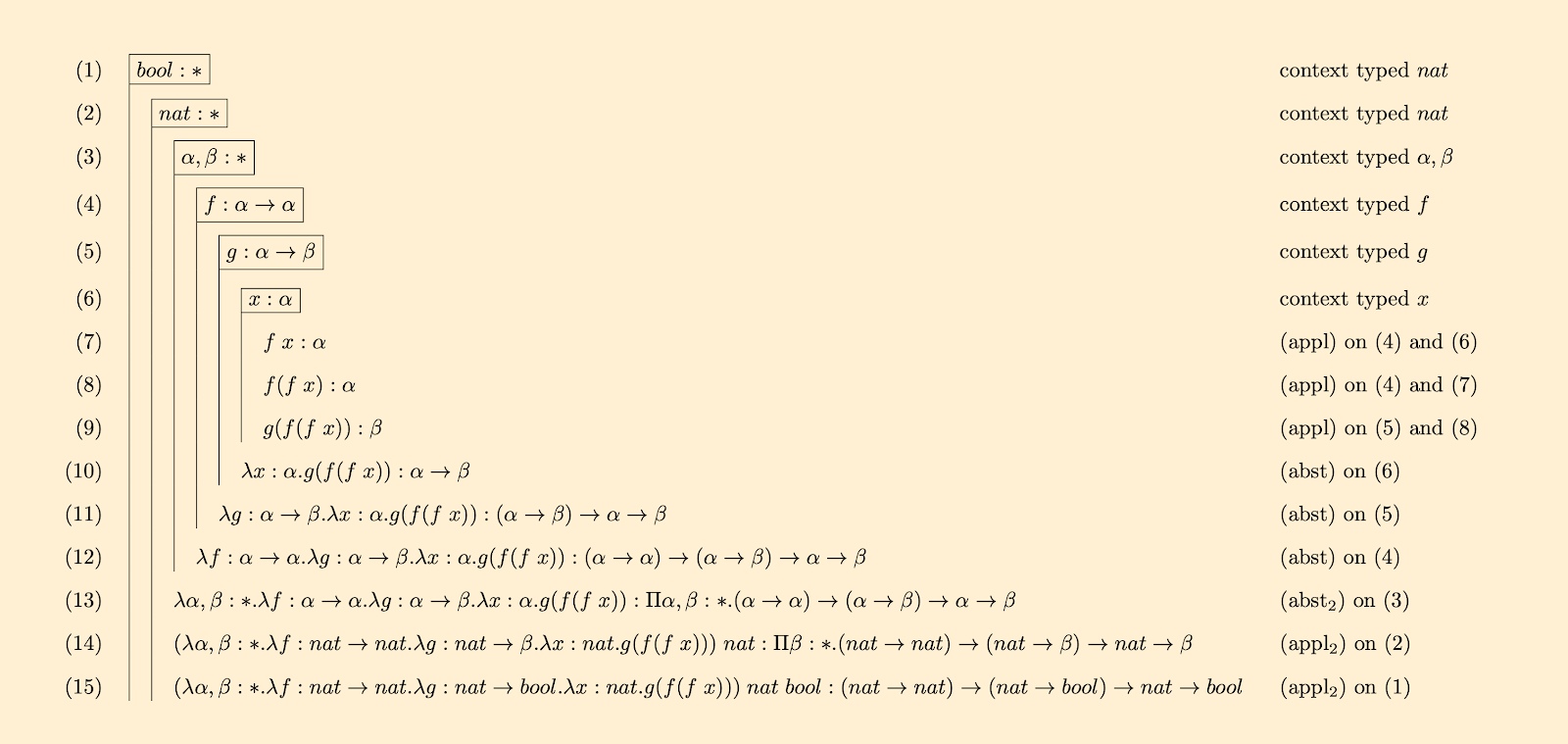Exercise 3.4
Give a shortened derivation in λ2 to show that the following term is legal in the context $Γ ≡ nat : ∗, bool : ∗$
$$(λα,β : ∗. λf : α →α. λg : α →β. λx : α. g(f(f x))) \; nat \; bool$$
The following is a derivation in flag format.
Given a context $Γ ≡ nat : ∗, bool : ∗$, the given term has type $(nat \to nat) \to (nat \to bool) \to nat \to bool$, and so the term is legal.