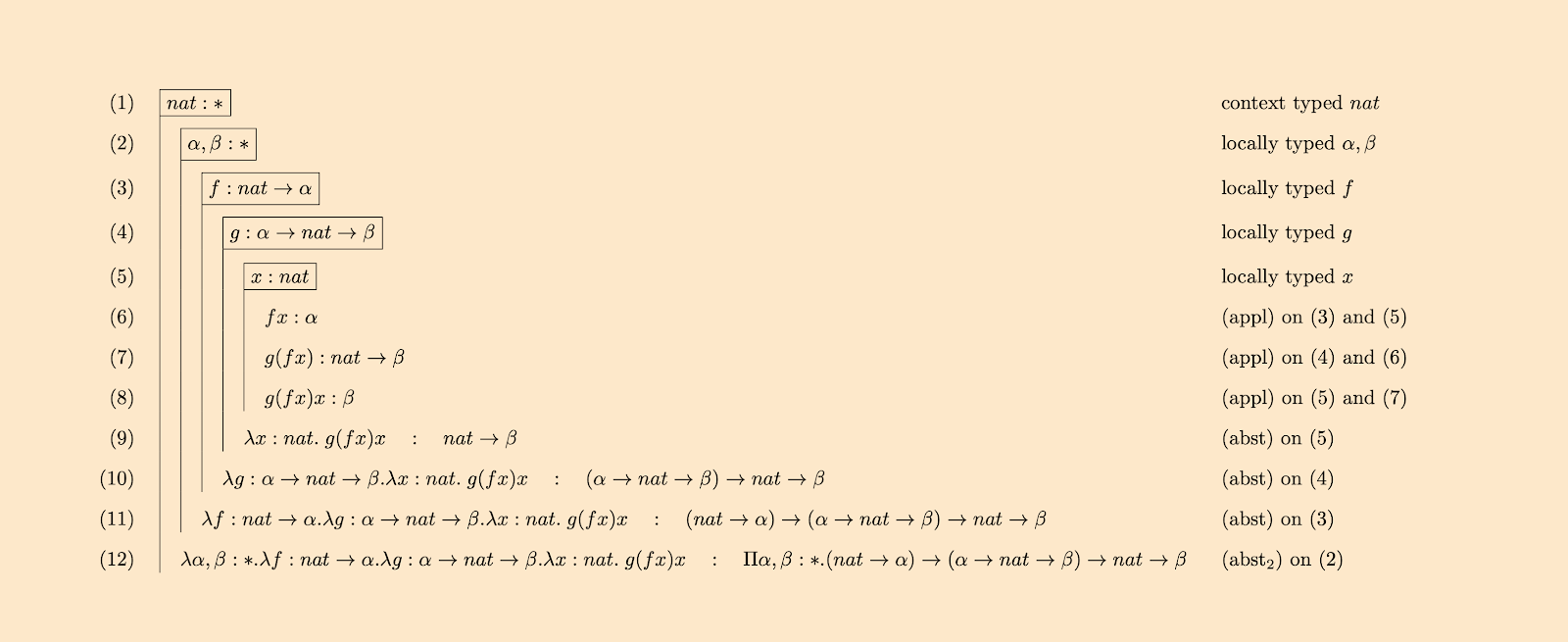Exercise 3.6
Find terms in $Λ_{\mathbb{T}2}$ that are inhabitants of the following λ2-types, each in
the given context $Γ$:
(a) $Πα,β : ∗. (nat →α) →(α →nat →β) →nat →β$, where $Γ ≡nat : ∗$
(b) $Πδ : ∗. ((α →γ) →δ) →(α →β) →(β →γ) →δ$, where $Γ ≡α : ∗, β : ∗, γ : ∗$
(c) $Πα,β,γ : ∗. (α →(β →α) →γ) →α →γ$, in the empty context.
(a) The following derivation in flag notation shows the following term is an inhabitant in the given context.
$$ \lambda \alpha, \beta :* .\lambda f: nat \to \alpha . \lambda g: \alpha \to nat \to \beta .\lambda x:nat .\; g(fx)x $$
(b) The following derivation in flag notation shows the following term is an inhabitant in the given context.
$$ \lambda \delta: *. \lambda f: (\alpha \to \gamma) \to \delta . \lambda g: \alpha \to \beta .\lambda h:\beta \to \gamma. f(\lambda x:\alpha . h(gx)) $$
(c) The following derivation in flag notation shows the following term is an inhabitant in the given context.
$$ \lambda \alpha, \beta, \gamma : * . \lambda f:\alpha \to (\beta \to \alpha) \to \gamma . \lambda x : \alpha . fx (\lambda y:\beta.x) $$